Wykresy kołowe oraz radarowe nie są preferowanymi pod względem szybkości pracy z danymi, ale są tymi, które wyglądają najbardziej atrakcyjnie na prostych dashboardach. Dlatego w wielu rozwiązaniach Business Intelligence (takich jak Tableau czy Power BI) użytkownicy wstawiają liczniki częściej niż wykres pociskowy. Zawsze jednak natrafiają na ten sam problem – jak pokazać na liczniku sumującym się do 100% przekroczenie planu? Wykres, który zaprezentuję, jest szczególny właśnie z powodu takiej możliwości. Co więcej, ma też ciekawą konstrukcję, opierającą się o nazwy zdefiniowane – dla zwykłego użytkownika Excel tak utworzony wykres będzie bardzo tajemniczy.
Więcej o licznikach możesz przeczytać w innych artykułach na ten temat:
- Jak utworzyć licznik w Excelu?
- Cztery wykresy, których należy unikać – w tym kołowy i radarowy
- Nie wymyślaj koła na nowo – o naszym uwielbieniu wszystkiego, co okrągłe
Przygotowanie danych
W przypadku tego wykresu danych nie potrzeba wiele. Pierwsza liczba to wskaźnik realizacji planu (wahający się w przypadku naszego przykładu od 0 do 199 – dla uproszczenia nie posługuję się wartościami procentowymi). Powiązane z nią jest pole Tytuł.
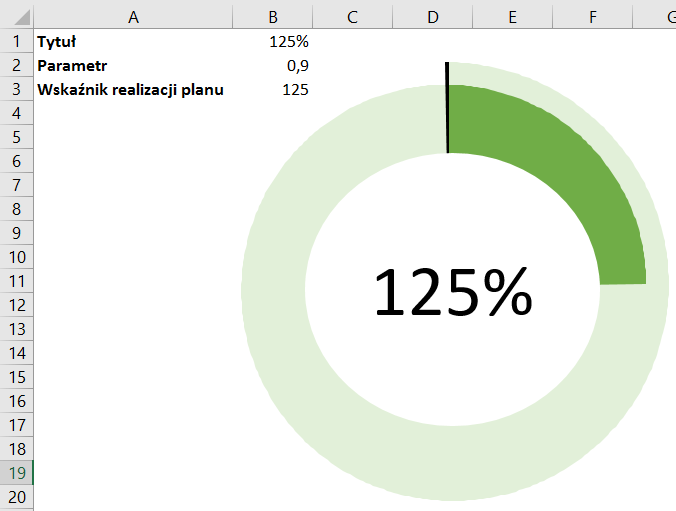
Pole Parametr to część, jaką będzie stanowić małe koło w stosunku do dużego.
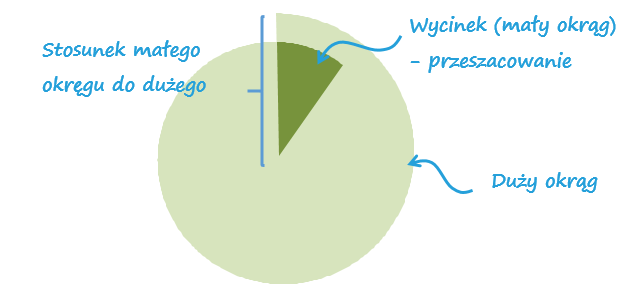
Tworzenie serii danych na wykresie radarowym
Wartościami osi x będą kolejne stopnie na okręgu, dlatego będę wyliczać wartości y dla 360 punktów na osi x (czyli okręgu). Wartości osi Y będą mieściły się w zakresie od 0 do 1, osią y będzie promień dużego, czyli zewnętrznego okręgu.
Wstawię trzy serie danych: dla zewnętrznego okręgu, dla wycinka danych oraz dla linii, która uzupełni duży okrąg (w dalszej części artykułu wyjaśni się cel jej użycia).
Pierwsza seria
Będzie to granica zewnętrzna okręgu. Promień tego okręgu stopniowo będzie się zmniejszać z kolejnymi stopniami od wartości 1 do 0,8 – czyli jednego z parametrów ustalonego na początku (część jaką będzie stanowił mały okrąg w stosunku do dużego okręgu).
Następującą formułę wprowadzam do komórki A1.
=1-(WIERSZ()-1)*(1-0,8)/360
– zaczynam od pierwszego wiersza we wprowadzeniu formuły , ponieważ mamy zagnieżdżoną wewnątrz formułę WIERSZ()
– wynikiem formuły jest promień okręgu na danym stopniu od 1 do 360 (czyli numeru wiersza)
– od 1 odejmujemy dla każdego stopnia (WIERSZ()-1) odpowiednią część różnicy pomiędzy dużym a małym okręgiem ((1-0,08)/360)
– podsumowując w każdym wierszu, czyli z każdym stopniem okręgu zbliżamy się do wartości 0,8
Druga seria
Stworzona jest tylko po to by w wierszu pierwszym oraz ostatnim (360) dawała wartość 1 dla uzupełnienia graficznego, serii danych dużego koła.
Do komórki C1 wpisuję formułę:
=(WIERSZ()=1)+(WIERSZ()=360)
Funkcja przyjmie wartość 1 w wierszu (i na stopniu) 1 oraz 360.
Trzecia seria
Będzie obrazowała wycinek z przeszacowaniem, formuła powinna dać zatem wynik tylko dla części z przeszacowaniem czyli dla naszego przykładu będzie to 10 % ((110-100)/100=10%), czyli 36 stopni (360 *10%) tylko dla zakresu 1-36 stopni kolorujemy wycinek (tylko w tych wierszach powinny być wartości oraz wiersza 360).
Do komórki B1 wpisuję formułę:
=(WIERSZ()<=3,6*(110-100))*(0,8-WIERSZ()*((1-0,8)/360))+(WIERSZ()=360)*(0,8-(1-0,8)/360)
– (WIERSZ()<=3,6*(110-100)) – pierwsza część gwarantuje, że wartości pojawią się w pierwszych 36 wierszach – czyli do 36 stopnia
– (0,8-WIERSZ()*((1-0,8)/360)) – podobnie jak w przypadku pierwszej serii ta część formuły pokazuje jak w zależności od wiersza, w której się znajduje okrąg dot. małego wycinka będzie proporcjonalnie przesuwał się w stosunku do dużego okręgu
– (WIERSZ()=360)*(0,8-(1-0,8)/360) – ta część formuły przewidziana jest dla ostatniego wiersza (360) tak by miał on taką samą wartość (y) jak w wierszu pierwszym – by wycinek był kompletny i ładnie wypełniony kolorem
Utworzenie wykresu
Pokazane formuły powinny znaleźć się w zakresie od A1 do C360. (kolumna A – pierwsza seria danych, kolumna B – druga seria danych, kolumna C – trzecia seria danych).
![]()
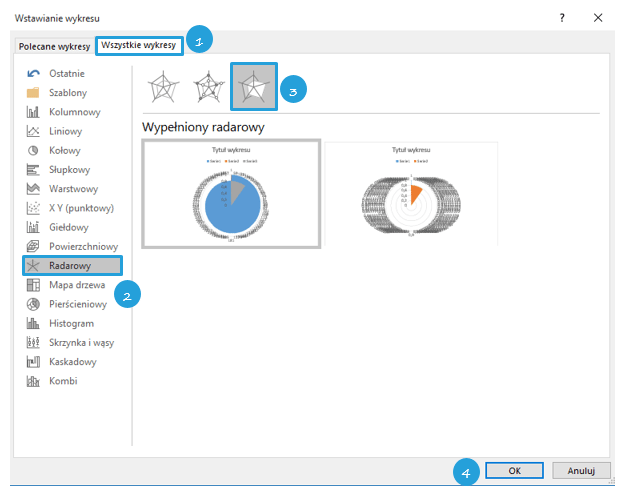
Zaznaczam dane, poprzez Wstawianie > Wykresy > Wyświetl wszystkie wykresy > Wszystkie wykresy

Radarowy > Wypełniony radarowy > OK
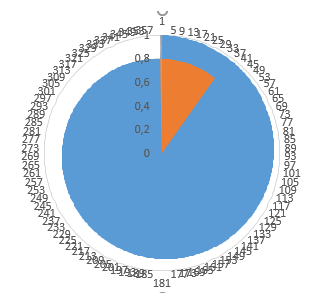
Przy powiększeniu wstawionego wykresu dokładnie widać serię numer 2– zaznaczona jest domyślnie na pomarańczowo.
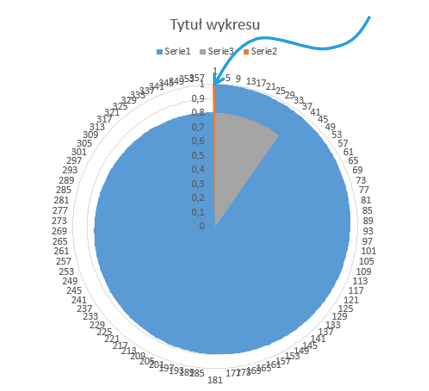
Poniżej widok co dzieje się gdy serię numer 2 usunę. Widać niewielką lukę pomiędzy danymi (360 a 1). Dlatego też potrzebna jest seria nr 2. Przywrócę ją teraz oraz nadam jej kolor (niebieski) taki sam jak dla serii numer 1.
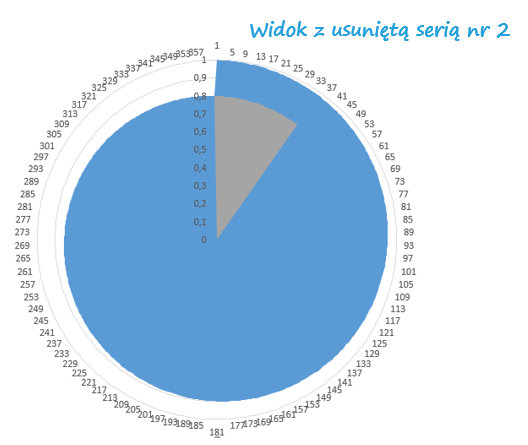
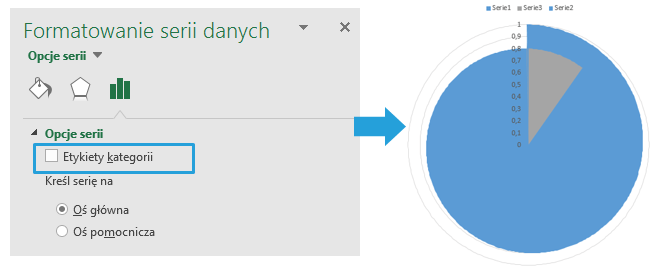
Wartości wokół koła to wartości osi x, natomiast pionowa oś o zakresie od 0 do 1 to oś y. Aby nie zaburzały widoku usuwam etykiety kategorii osi x oraz y. Zaznaczam wykres > Formatowanie serii danych > Opcje serii > Etykiety kategorii > Odznaczam. Dzięki tej operacji usuwam kategorie osi x.
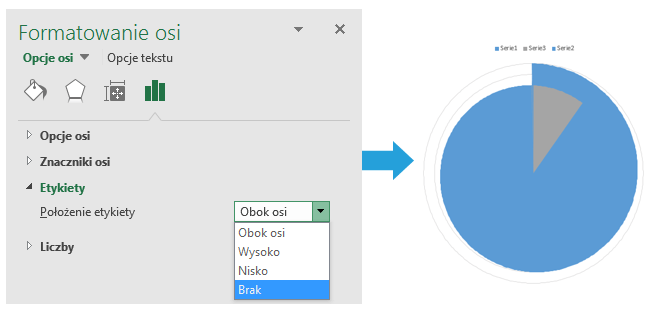
Aby usunąć kategorie osi y, zaznaczam je na wykresie > prawy przycisk myszy > Formatuj oś

Formatowanie osi > Etykiety > Położenie etykiety > Brak
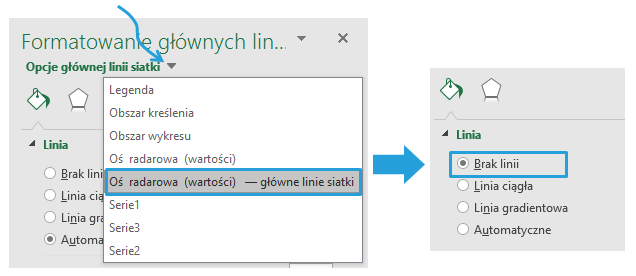
Do usunięcia pozostaną jeszcze wciąż widoczne linie siatki. Zaznaczam wykres > Formatowanie > Oś radarowa (wartości) – główne linie siatki > Linia > Brak Linii
Na takim etapie można by zakończyć omówienie tematu, ale obiecałem jeszcze trik.
Efekt magiczny – ukrycie serii pod nazwami zdefiniowanymi
Gdybyśmy taki wykres budowali zwykłym sposobem, nasz arkusz z danymi wyglądałby tak:
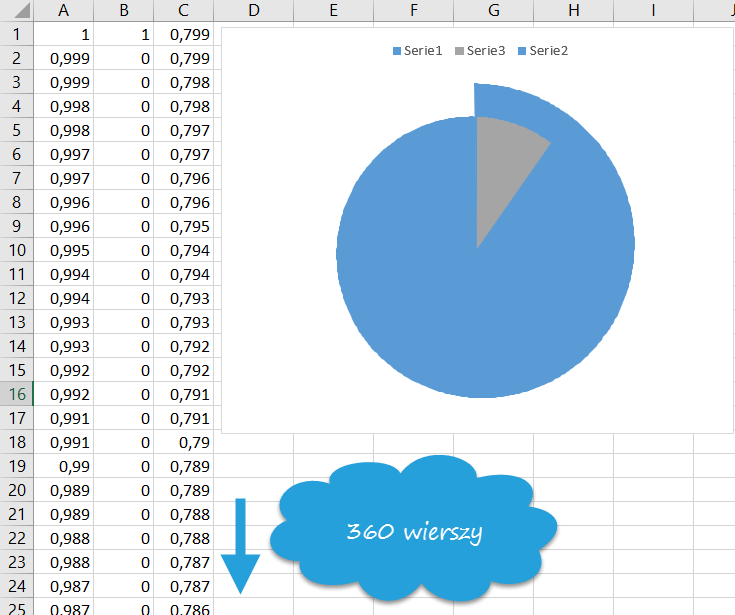
Ja jednak zakresy (czyli serie danych) ukryję w Menedżerze nazw, pod nazwami zdefiniowanymi, jednocześnie unifikując formuły. Dzięki temu będą zależne tylko od wspomnianych na początku dwóch parametrów:
- stosunek małego koła do dużego – „Parametr” – wartość w komórce B2 – 0,
- stopnia wykonania planu – „Realizacja” – wartość w komórce B3 – 125
Parametry te wprowadzam od razu do Menedżera nazw. Formuły > Nazwy zdefiniowane > Menedżer nazw >

Nowy >
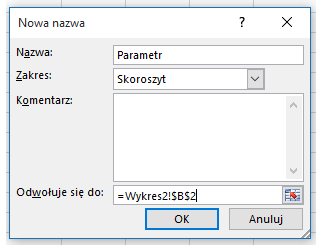
wprowadzam nazwę „Parametr” oraz odwołanie do komórki > OK. Takie same kroki wykonam dla drugiego parametru.
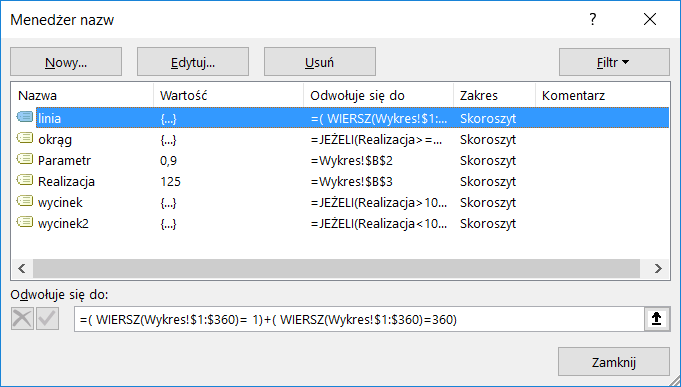
W wyniku działań w menedżerze posiadam dwa zdefiniowane zakresy jak poniżej:
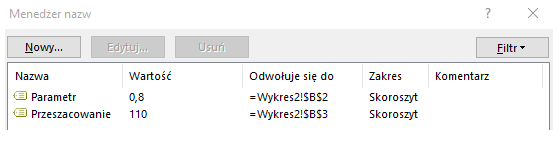
Kolejnym krokiem będzie zmodyfikowanie wcześniej stworzonych formuł, w taki sposób by odwoływały się do utworzonych nazw zdefiniowanych oraz działały wewnątrz menedżera a nie na zakresie komórek.
Seria 1
1-(WIERSZ()-1)*(1-0,8)/360
– WIERSZ() zamieniam na WIERSZ($1:$360) – dlaczego? W nazwach zdefiniowanych do obliczenia wartości w seriach danych użyję formuł tablicowych, które pozwolą na uniknięcie zamieszczania formuł w kolejnych komórkach i w miejsce WIERSZ($1:$360) pojawi się tablica wartości <1;360>
– 0,9 zmieniam na zdefiniowaną nazwę czyli „Parametr”
Formuła po naniesionych zmianach będzie miała formę
=1-(WIERSZ($1:$360) -1)*(1-Parametr)/360
Wprowadzam ją do menedżera pod nazwą okrąg, pamiętając by po zakończeniu wpisywania formuły wybrać na klawiaturze Ctrl+Shift+Enter , co uruchomi formuły tablicowe. Uruchomienie formuł tablicowych będzie też widoczne w menedżerze (w kolumnie wartość nawias klamrowy).

Podobnie działam z serią 2 i 3.
Seria druga przed
=(WIERSZ()=1)+(WIERSZ()=360)
Oraz po
=( WIERSZ($1:$360)= 1)+( WIERSZ($1:$360)=360)
Będzie to nazwa zdefiniowana „linia”.
Seria trzecia przed
=(WIERSZ()<=3,6*(110-100))*(0,8-WIERSZ()*((1-0,8)/360))+(WIERSZ()=360)*(0,8-(1-0,8)/360)
oraz po
=( WIERSZ($1:$360)<=3,6*(Przeszacowanie-100))*(Parametr- WIERSZ($1:$360)*((1-Parametr)/360))+( WIERSZ($1:$360)=360)*(Parametr-(1-Parametr)/360)
nazwa zdefiniowana dla tej serii do „wycinek”.
Kiedy wszystkie serie-nazwy są już zdefiniowane, przechodzę do umieszczenia ich na wykresie. Aby wstawić wykres zaznaczam dane dot. zmiennych parametrów (w innym wypadku nie przejdę do okna wstawiania i wyboru wykresu). Wybieram jak wcześniej ten sam typ wykresu (radarowy wypełniony).
Zaznaczam wstawiony wykres > prawy przycisk myszy > Zaznacz dane > zaznaczam istniejącą serię i ją usuwam.

Następnie wybieram > Dodaj i umieszczam nowe własne zdefiniowane serie. Poniżej pierwszy przykład zdefiniowanej nazwy wykorzystanej jako seria danych.
UWAGA!!!
Należy pamiętać o konstrukcji odwołania do nazwy – wskazuję arkusz w którym zdefiniowana jest zmienna.
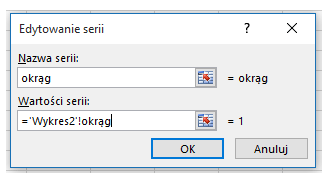
Te same kroki powtarzam dla kolejnych serii.
I voila! Wykres taki sam jak przy pierwszym sposobie. Należy go jedynie sformatować, ale tu już kroki i możliwości zostały wcześniej omówione. Wykres jest jednak po upgrade ponieważ, jest teraz uzależniony od wartości w komórkach B2 oraz B3. Można łatwo sprawdzić jak się zmieni w zależności od wartości tych parametrów.
Stosując tę technikę finalnie utworzyłem dodatkową serię, która odpowiada za wartość, gdy plan nie został zrealizowany i nazwałem ją wycinek2.
Przykład wykorzystania na dashboardzie menedżerskim
Dodając do tak przygotowanego wykresu radarowego autokształt koło z wartością KPI jako etykietą (w połączeniu z komórką Tytuł), otrzymujemy licznik. Pamiętajmy, że działa on dla wartości z zakresu 0-199 – przy podwójnym „przekręceniu zegara” trzeba by wprowadzić dodatkowe modyfikacje.
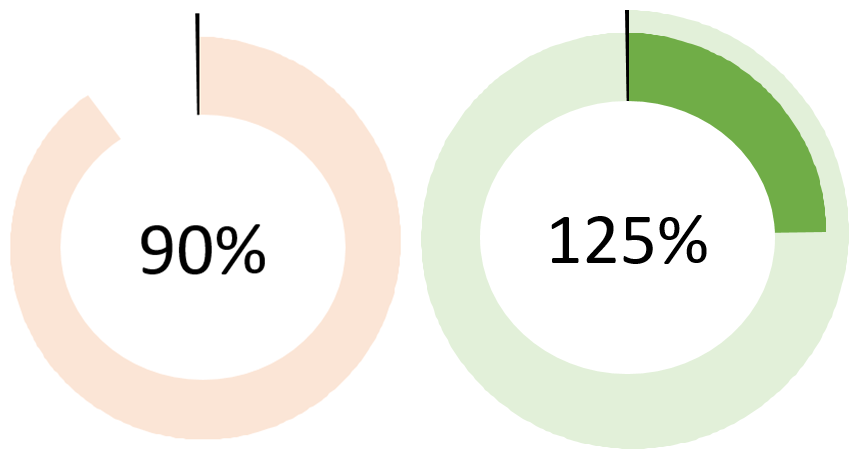
Pobierz szablon licznika Excel
Tu możesz pobrać gotowy szablon licznika Excel i wykorzystać go do budowy dasbhoardu menedżerskiego.


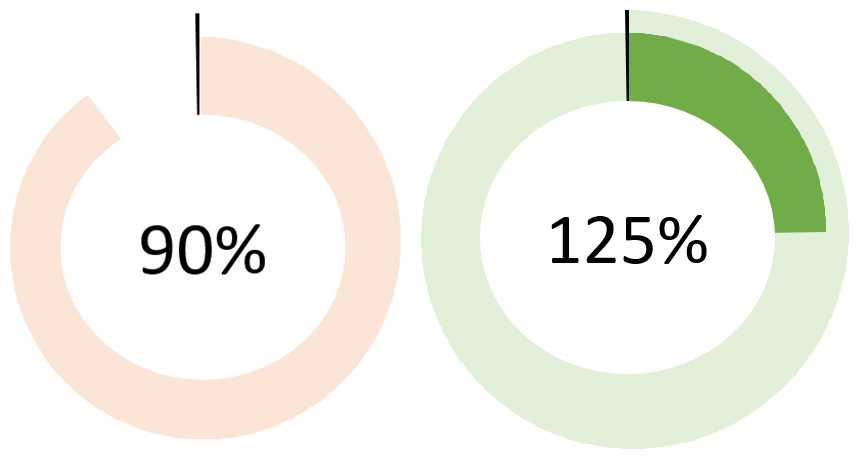



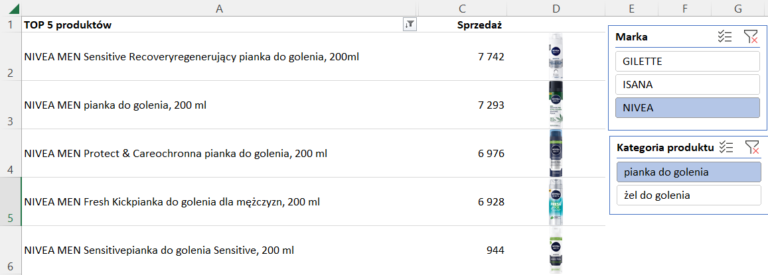
Wykres bardzo fajnie się prezentuje, niestety według zamieszczonego opisu nie jestem w stanie go skonstruować.
Przekazane wiadomości są niespójne, opisują jedno a zamieszczone screeny pokazują zupełnie coś innego.
Pozdrawiam.
Proponuję pobrać szablon i zerknąć w kod, bo rzeczywiście przy pisaniu artykułu powstało kilka wersji wykresu końcowego.