Wybór odpowiedniej skali do prezentowania danych na wykresie jest niezwykle ważny. Niekiedy wybór złej skali uniemożliwia wręcz porównania danych, szczególnie tych, charakteryzujących się wartościami z rozległego przedziału liczbowego – w takim przypadku skorzystanie ze skali liniowej byłoby nieefektywne, osie (x, y bądź obie) musiałaby być tak długie, aby zmieścić wszystkie wartości. Najlepszym rozwiązaniem będzie więc zastosowanie skali logarytmicznej.
Definicja skali logarytmicznej
Skala logarytmiczna jest rodzajem skali pomiarowej, w której mierzona wartość zostaje przekształcona za pomocą logarytmu. Wartości tej skali są bezwymiarowe, co oznacza że są podawane w odniesieniu do pewnej jednostki bądź są logarytmami wielkości niemianowanych. Skala powinna posiadać zdefiniowaną używaną podstawę logarytmu. Skala logarytmiczna jest używana tylko do odwzorowania wielkości dodatnich. Najczęściej używane są logarytmy dziesiętne, o podstawie równej 10, oraz logarytmy naturalne – podstawa równa e. A logarytm jest niczym innym niż stosunkiem (łac. logarithmus) i proporcją (gr. logos). Logarytm (dziesiętny) to wykładnik potęgi, do której należy podnieść liczbę 10, aby otrzymać liczbę logarytmowaną.
Kiedy stosujemy skalę logarytmiczną
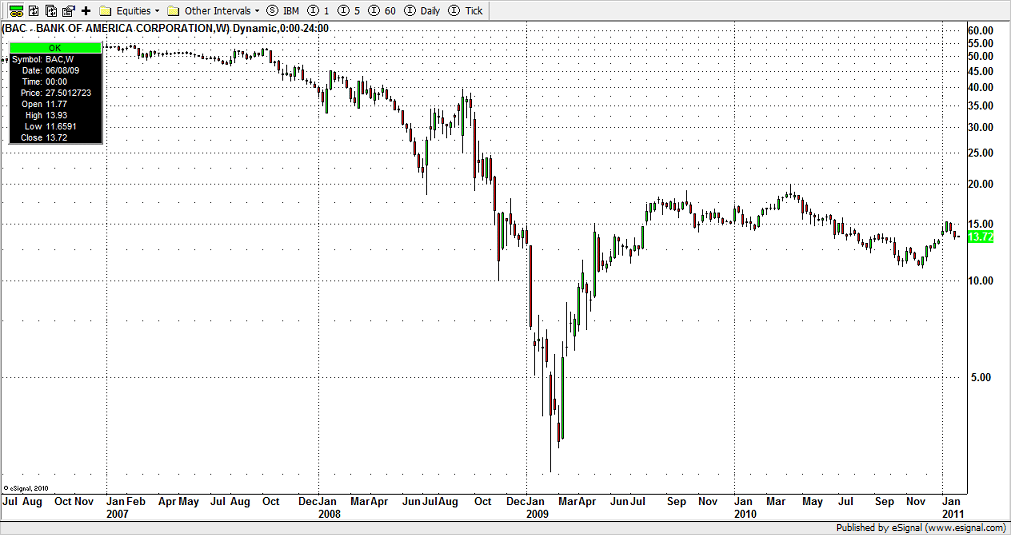
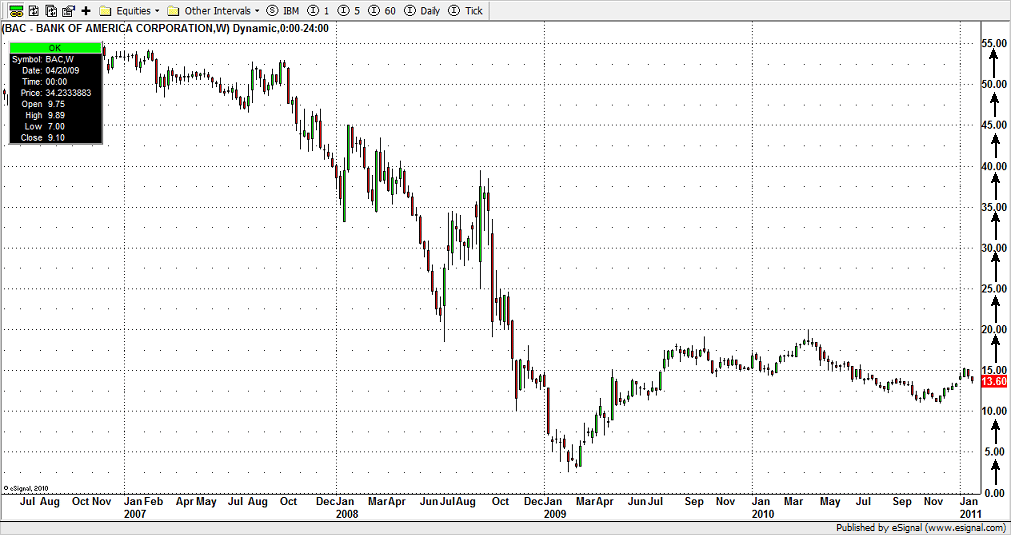
Skala logarytmiczna powinna być stosowana w przypadku analizy wartości, między którymi są bardzo duże różnice. Korzystanie z omawianej skali umożliwia utworzenie podziałki o równomiernie rozłożonych liniach, ale rosnących albo malejących wartościach. Skala logarytmiczna umożliwia pokrywanie dużego zakresu wartości, ma dużą rozdzielczość. Są dwa główne powody, aby stosować skalę logarytmiczną na wykresie. Pierwszym z nich jest wspominana już duża różnica pomiędzy analizowanymi wartościami. Drugim powodem jest pokazanie procentowej zmiany wielkości lub odziaływania na siebie prezentowanych czynników. Dobrym przykładem do wytłumaczenia potrzeby używania skali logarytmicznej będzie analiza danych giełdowych, a dokładnie analiza cen akcji. Skala liniowa przedstawiałaby równą odległość pomiędzy równymi odstępami cen. Wzrost ceny z 20 do 30 złotych będzie prezentowany tak samo jak zmiana z 120 do 130 złotych. W pierwszym przypadku zmiana ta to 50%, a w drugim to tylko ok. 8%. Inwestor będzie na pewno bardziej zainteresowany dynamiką zmian. Chce, aby zysk, mierzony procentowo, był jak największy. Dlatego też na rynkach finansowych używa się skali logarytmicznej, która pokazuje w równych odległościach te same zmiany procentowe. Odległość pomiędzy 20 a 30 złotych będzie taka sama, jak między 200 a 300 złotych. Wykres giełdowy w skali logarytmicznej:
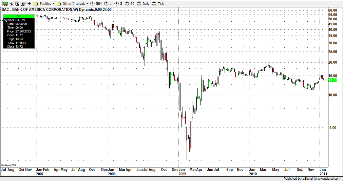
Wykres giełdowy w skali liniowej:
źródło: www.day-trader.pl
Skala liniowa a logarytmiczna
Skala liniowa przedstawia równe odległości pomiędzy wartościami. Poniższa oś rozpoczyna się od 0, kolejną wartością jest 10, a następną 20. Widzimy, że odcinki między 0 a 10 oraz 10 a 20 są równe. Gdyby analizowane wartości byłyby z przedziału 0 – 1 000 000 i korzystalibyśmy z poniższej skali liniowej, oś musiałaby 50 000 razy dłuższa.
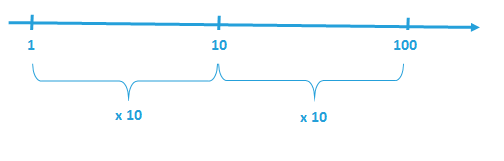
Skala logarytmiczna umożliwia analizowanie danych z rozległego przedziału. Poniższa oś rozpoczyna się od 1, następną wartością jest 10, a kolejną 100. Wygląda to tak, ponieważ wartości multiplikują się wzajemnie, a wynikiem jest kolejna wartość.
Kolejną wartością na osi byłby wynik działania 100 x 10, czyli 1000.
Jak widzimy na powyższym wykresie . Inaczej można to zapisać Ogólny wzór logarytmu dziesiętnego to:
Plusy i minusy wykresu logarytmicznego
Skala logarytmiczna ma szersze zastosowanie w przypadku analiz średnio i długoterminowych oraz do wyznaczania linii trendu. Dodatkowo skala ta sprawdza się, jak było już wspomniane, do prezentowania danych z rozległego przedziału liczbowego. Ponadto umożliwia poprawną analizę dynamiki zmian wartości. Wadą może być nieumiejętność czytania danych z wykresu ze skalą logarytmiczną. Dodatkowo należy zwracać uwagę na nierówne odległości pomiędzy wartościami. Wykorzystajmy ostatnią oś do zobrazowania pułapek czyhających na twórcę i odbiorcę wykresu.
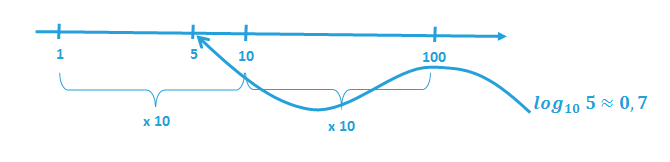
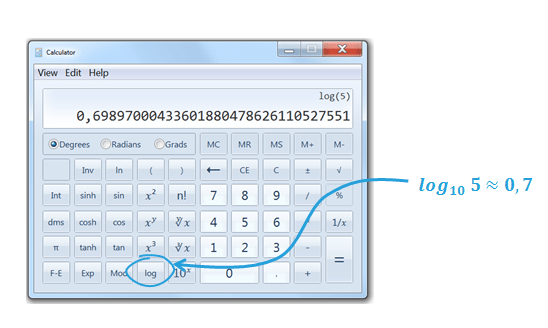
Gdybyśmy chcieli na osi zaznaczyć wartość 5, nie możemy po prostu zaznaczyć odcinka w połowie pomiędzy wartością 0 a 10. Logarytm dla 5 należy obliczyć. Możemy skorzystać z kalkulatora systemowego (zmieniamy tylko Widok > Naukowy).
Jak widzimy odległość ta będzie wynosiła ok 0,7 długości odcinka, a nie 0,5 jak w skali liniowej.
Skala logarytmiczna – stosować czy nie?
Podsumowując rozważania na temat skali logarytmicznej, stwierdzamy, że jest to skala, która nadaje się do stosowania dla wąskiego grona odbiorców – analityków, którzy będą wiedzieli o jej wadach i zaletach. W większości przypadków stosujmy skalę liniową.
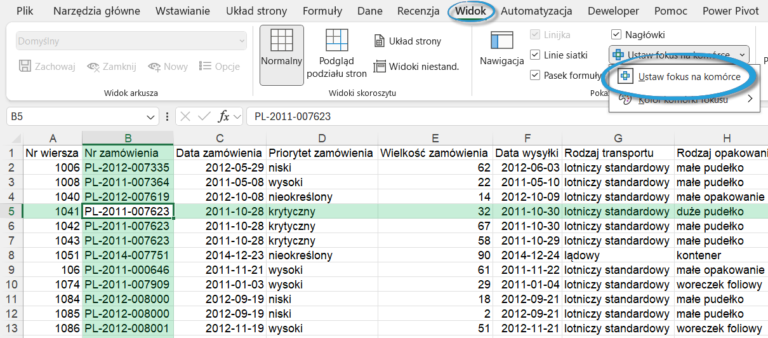
Jak zmienić typ osi na logarytmiczny w programie Excel?
W Excelu stosowanie skali logarytmicznej jest dużo wygodniejsze niż ręczne wyliczanie wartości, ale o tym w kolejnym artykule już wkrótce.
Materiał jest co najwyżej przeciętny, operacje zrobione, wytłumaczenie jest zbyt słabo opisane i nie ma np na wykresach opisu jednostek etc. Teraz ktoś kto to czyta nie zna tematu, nie wie jak ma to rozumieć i musi to rozkminiać na milion możliwości co to oznacza, albo skąd się to bierze.
Przeciętny artykuł? Raczej bardzo słaby! O ile o zastosowaniach jest w miarę OK, to tłumaczenie na czym polegają skale to po prostu masakra. „Skala liniowa przedstawia równe odległości pomiędzy wartościami.” Ale jakimi wartościami? Przecież w skali logarytmicznej też odległości pomiędzy wartościami 10, 100, 1000 itd. są równe!
„Wygląda to tak, ponieważ wartości multiplikują się wzajemnie, a wynikiem jest kolejna wartość.” – co za bzdury! Czyli po 10 jest dajmy na to 100, po 100 jest 10*100=1000, a następna wartość ma być 100*1000? Jak wzajemnie, to wzajemnie!
Do usunięcia jak najszybciej! Autor wybrał bardzo ciekawy temat, ale nie podołał temu trudnemu zadaniu!