Dziś mały wstęp do statystki a być może dla Ciebie powrót? Otóż tymi rzadziej wykorzystywanymi kalkulacjami w tabeli przestawnej są miary statystyczne czyli odchylenie standardowe oraz wariancja. By móc je zastosować należy wiedzieć czym są 🙂 Zatem w tym artykule wyjaśniam co rozumiem pod nazwą średniej, odchylenia standardowego oraz wariancji (nieco wiedzy statystycznej znajdziesz we wpisie o wykresie Gaussa). Do czego i w jaki sposób będzie można je zastosować?
Wyjaśnienie pojęć statystycznych
Sztuką jest przekazać wiedzę niełatwą w przystępny sposób, czyli np. statystykę. Spróbuję a ocenisz sam/a…
- Średnia – od niej należy zacząć, najczęściej rozumiana jako średnia arytmetyczna, czyli suma wartości zmiennych danego zbioru podzielona przez liczbę tych zmiennych, jest miarą tendencji centralnej czyli miejsca największej koncentracji wyników.
- Odchylenie standardowe – zaraz po średniej najczęściej stosowane pojęcie statystyczne. Odchylenie mówi jak daleko od średniej rozrzucone są wartości w danym zbiorze – im odchylenie jest mniejsze tym wartości są bardziej skupione wokół średniej. Odchylenie jest pierwiastkiem z wariancji.
- Wariancja – mówi o rozproszeniu wyników – czy są skoncentrowane wokół średniej, czy może od niej oddalone. Gdy wynosi zero, oznacza to, że wyniki nie są w ogóle zróżnicowane. Częściej stosowane od niej jest odchylenie standardowe.
Obliczenia w tabeli przestawnej
Warto pamiętać, że nie muszę w tabeli przestawnej tworzyć pola obliczeniowego by obliczyć odchylenie standardowe, ponieważ jest to możliwe wśród wbudowanych narzędzi tabeli przestawnej.
Aby dostać się do ustawień pola wartości tabeli przestawnej wybieram jedną z możliwości:
- w polach tabeli przestawnej, w obszarze wartości wybieram jedno z pól > wciskam strzałkę po prawej stronie (włączam menu podręczne) > ustawienia pola wartości
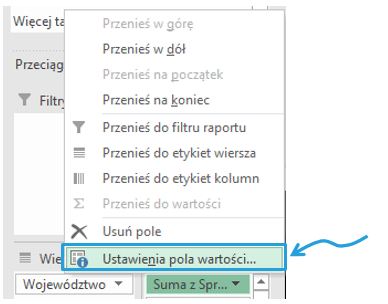
- klikając prawym przyciskiem myszy w obszarze raportu tabeli przestawnej > ustawienia pola wartości
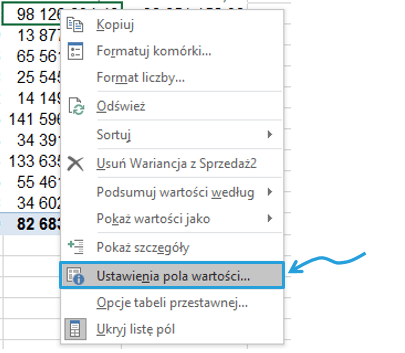
Poniżej okno ustawień pola wartości , oprócz popularnie używanych: sumy czy licznika, znajdują się tu również Odchylenie standardowe, Odchstdc, Wariancja oraz Wariancja populacji.
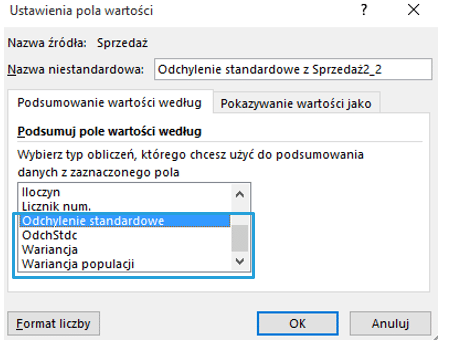
Nazwy bardzo podobne, jednak znaczenie miar nieco inne.
- Odchylenie standardowe, Wariancja – używam gdy dane na których pracuję są tylko wycinkiem całości, czyli podzbiorem populacji.
- OdchStdc, Wariancja populacji – gdy badany element jest całą populacją (nie jest wycinkiem).
Wśród rzadziej używanych kalkulacji w tabeli przestawnej oprócz miar statystycznych znajdują się:
- Iloczyn – (ang. Product) jak sama nazwa mówi to iloczyn wartości, jeżeli dane pole nie zawiera liczb a np. tekst wówczas iloczyn wynosi zero. Do czego można wykorzystać iloczyn? Np. do obliczenia średniej geometrycznej.
- Licznik num. – zliczenie wartości, które są liczbami , zlicza wystąpienia liczb, czyli jeżeli w danej kolumnie oprócz liczb znajdzie się tekst, wówczas nie zostanie on zliczony. Tę funkcję można wykorzystać do szybkiego sprawdzenia formatu w danych – porównując wartość Licznik num. z ilością wierszy w źródłowej tabeli.
Zastosowanie miar statystycznych w tabeli przestawnej
Posiadając wiedzę na temat poszczególnych miar statystycznych, mogę wykorzystać je do analizy danych w tabeli.
Poniżej tabela z danymi dot. sprzedaży w podziale na segmenty rynku (korporacje, małe firmy, osoba fizyczna, biuro w domu). Zamieściłem w niej sumę ze sprzedaży, średnią oraz po dwa typy odchylenia standardowego oraz wariancji.
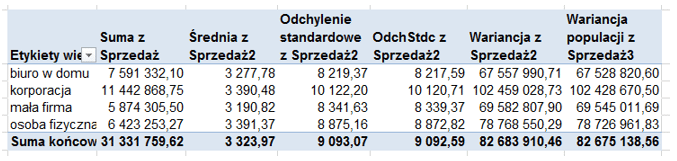
Na pierwszy rzut oka, średnie dla poszczególnych segmentów nie odbiegają zbytnio od siebie. Dzięki odchyleniu standardowemu mogę powiedzieć więcej o danych. Największe odchylenie występuje w segmencie korporacyjnym – co oznacza że występują w nim największe odchylenia od średniej, dane są najbardziej rozproszone (mamy jednocześnie bardzo niskie wartości sprzedaży jak i bardzo wysokie).
W segmencie gdzie odchylenie standardowe jest wysokie a średnia w porównaniu do innych segmentów jest porównywalna, można podejrzewać, że średnia jest błędną miarą wartości centralnej i być może należy wybrać inną np. medianę, dominantę, która lepiej zobrazuje zmienność wartości w segmencie.
Dzięki regule 3sigm (99,7% obserwacji znajduje się w odległości +/- 3 odchyleń standardowych od średniej) , odchylnie standardowe pozwala na odrzucenie ze zbioru danych wartości odstających, które mogą zniekształcać pomiary.
Dodatkowe korzyści daje również zamieszczenie odchylenia w tabeli przestawnej, ponieważ dane z łatwością można drążyć, poprzez dodanie kolejnych pól w obszarze wierszy. Poniżej pogłębienie analizy o regiony, dla segmentu korporacji. Widać, że to głównie region południowy generuje największą zmienność.
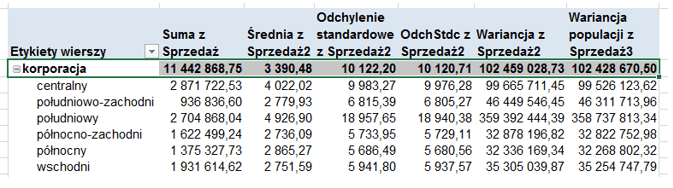
Bazę którą tu analizuję, traktuję jako całą populację, nie jako jej podzbiór, więc adekwatnymi miarami będą OdchStdc oraz Wariancja populacji – stosowane dla całych populacji.
Średnia a odchylenie standardowe na wykresie
Spróbuję pokazać regułę 3sigm na wykresie, również z oznaczeniem średniej. Dane pochodzą ze strony NBP i są to dzienne kursy euro w 2016 roku. Ponieważ kursy są podane z dokładnością do 4 miejsc po przecinku, zaokrąglam je do dwóch miejsc by później móc je zagregować (przy czterech miejscach, praktycznie żaden z kursów się nie powtarza).

Następnie w kolumnie G przeklejam jako wartości zaokrąglone kursy i usuwam z nich duplikaty. W kolumnie H zliczam ilość wystąpień każdego z kursów na przestrzeni całego roku. Ilość wystąpień oraz nieduplikujące się kursy posłużą mi do budowy wykresu.
Zaznaczam zakres G1:H29 > Wstawianie > Wykresy > Wykres punktowy.
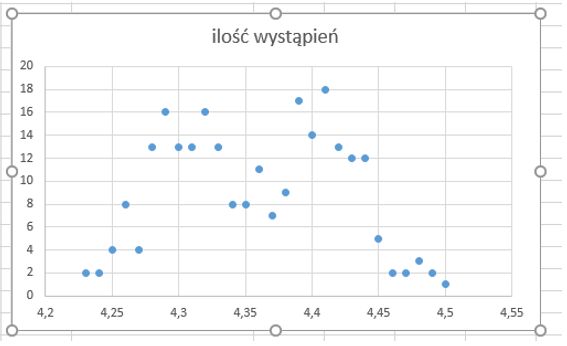
W komórkach L2 oraz L3 znajduje się odpowiednio średnia oraz odchylenie standardowe.
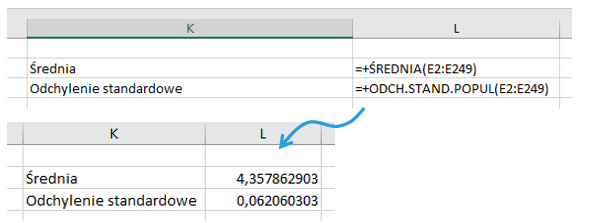
Wartości te wykorzystam do zaprezentowania reguły 3sigm czyli zakresu 3 odchyleń standardowych +/- od średniej. Średnią również zamieszczę na wykresie. Zatem zaczynam od przygotowania danych dla poszczególnych serii.
Dane dla średniej będą wyglądały jak poniżej:
Do wykresu dodam nową serię danych – Średnią. Prawym przyciskiem myszy klikam w obszarze kreślenia i z menu podręcznego wybieram > Zaznacz Dane.
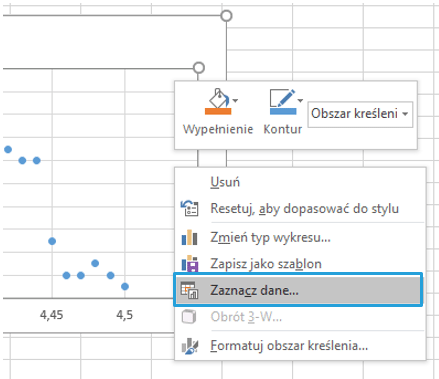
Wybieram Dodaj
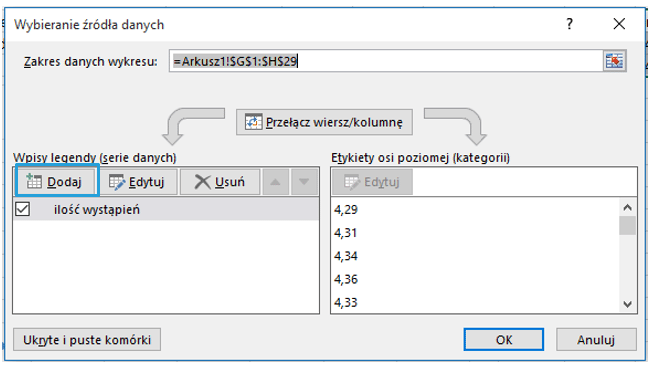
Uzupełniam okno Edytowanie serii odwołaniami do odpowiednich komórek > OK > OK.
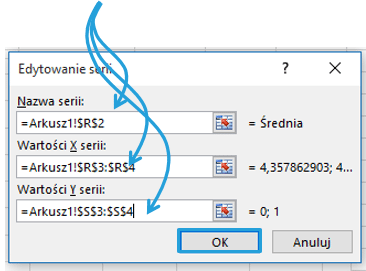
Na wykresie pojawiły się dwa punkty – zmienię je na linię prezentowaną na pomocniczej osi Y. Wybieram kartę Projektowanie > Typ > Zmień typ wykresu.
W oknie Zmienianie typu wykresu wybieram > Wszystkie wykresy > Kombi.
Dla serii danych „Średnia” wybieram oś pomocniczą i wykres punktowy z wygładzonymi liniami a dla ilości wystąpień – wykres punktowy> OK.

Odrywam poziomą linię pomocniczą wybierając plus przy wykresie.
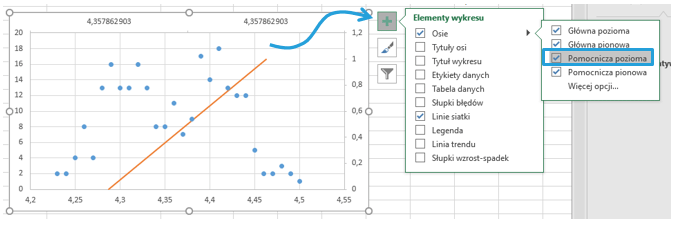
Zaznaczam poziomą oś pomocniczą > Formatowanie Osi > Opcje osi > Opcje osi > oś daty – dzięki temu pomarańczowa linia będzie pionowa.
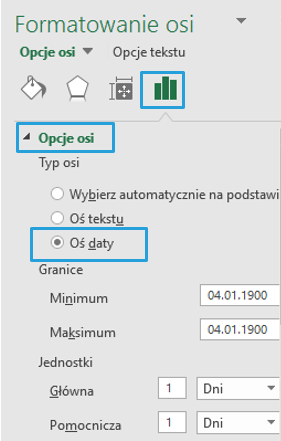
Również klikając podwójnie na pionową oś pomocniczą wybieram Formatowanie Osi > Opcje osi > Opcje osi . Jako Maksimum wpisuję 1> Enter.
Dzięki czemu Seria danych „Średnia” na wykresie prezentuje się jak poniżej.
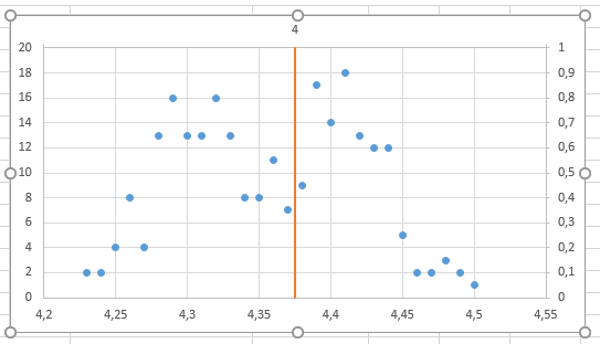
Tworzę jeszcze dwie serie – dla dolnej i górnej granicy przedziału (+/- 3 odchylenia standardowe od średniej). Będę je prezentować na osiach głównych więc wartości osi Y podaję od 0 do 20. Analogicznie jak wcześniej dodaję obie serie danych do wykresu i zmieniam dla nich typ na punktowy z wygładzonymi liniami. Po dodaniu obu serii automatycznie zmieni się wartość maksymalna na osi Y , wówczas należy w Formatowaniu osi i jej Opcjach zmienić maksimum na 20 (wskazówka poniżej).
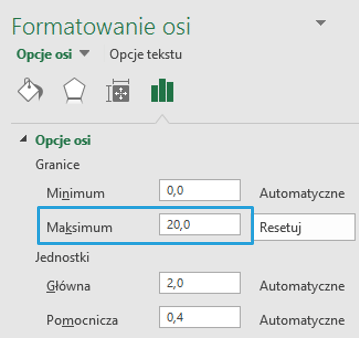
Po zmianach kolorystycznych wykres prezentuje się następująco:

Widać że wszystkie pomiary (punkty) mieszczą się w przedziale 3 odchyleń standardowych od średniej.
Pobierz plik Excel
Pobierz plik Rzadziej używane kalkulacje w tabeli przestawnej i umieść własne dane.