Szereg czasowy to pojęcie ze statystyki oznaczające ciąg obserwacji, który ukazuje kształt badanego zjawiska w kolejnych okresach (dniach, miesiącach, latach). Szereg czasowy to więc każdy wykres z osią czasu, na którym obserwacje są zbierane w regularnych odstępach. Jak pokazały badania, 80% wykresów tworzonych w firmach i organizacjach zawiera właśnie aspekt czasowy danych. Rysując szereg czasowy warto pamiętać, aby czas był na osi x i płynął od lewej do prawej (zasad 14 z infografiki „25 zasad wizualizacji danych”). Jak dodać wartość do analizy szeregu czasowego? Rozkładając go na składniki pierwsze i tworząc prognozę.
W szeregu czasowym można wyróżnić m.in.:
- Tendencję rozwojowa (trend) – wyraża ona skłonność do jednokierunkowych zmian (spadku lub wzrostu);
- Wahania cykliczne – długookresowe, rytmiczne wahania wokół tendencji rozwojowej;
- Wahania sezonowe – wahania wokół tendencji rozwojowej w okresie nieprzekraczającym roku;
Dekompozycja szeregu czasowego składa się na proces przewidywania pewnych zjawisk. W przypadku prognozowania na podstawie szeregu czasowego proces ten odbywa się poprzez stworzenie odpowiedniego modelu.
Budowa modelu szeregu czasowego w Excelu
Jak powyższą teorię przełożyć na analizę danych w Excelu? Za dane źródłowe posłuży informacja dotycząca wartości sprzedaży artykułów biurowych dla czterech segmentów: biuro w domu, korporacji, małych firm oraz osób fizycznych. Dane sprzedażowe dotyczą czterech lat 2011-2014 i są w rozbiciu miesięcznym. Na podstawie tych danych historycznych zostanie przygotowana prognoza na lata 2015-2016.
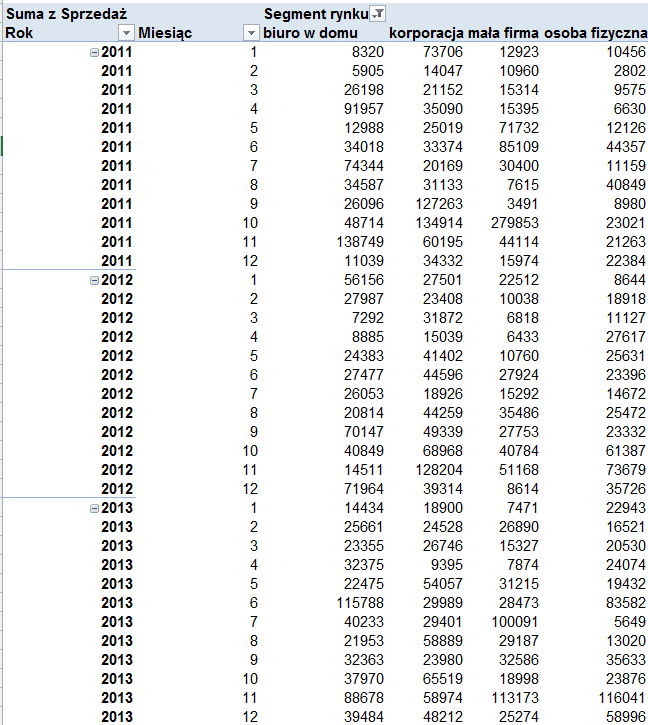
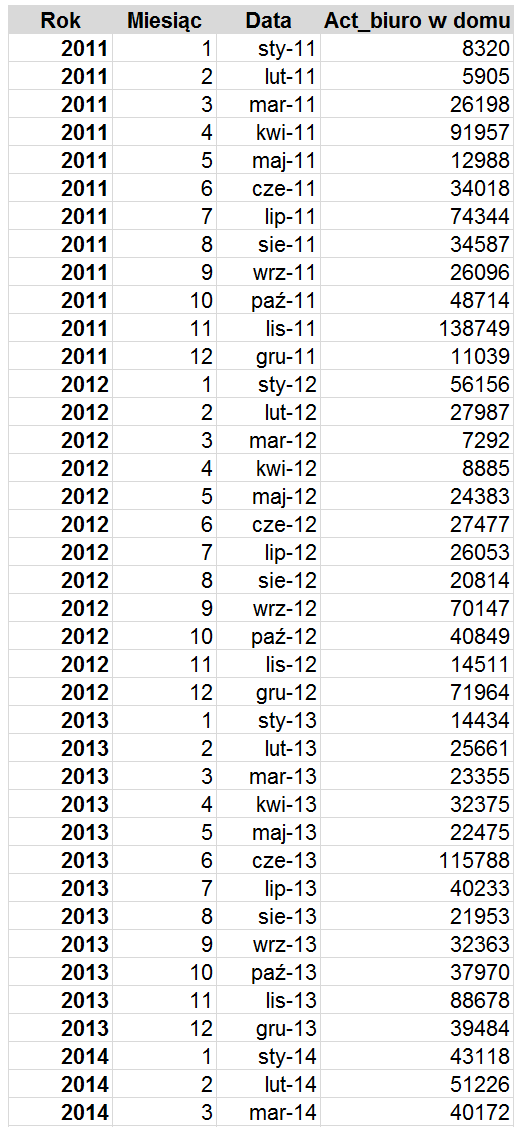
Przyjrzyjmy się najpierw sprzedaży artykułów biurowych do domowych biur. Przed wykorzystaniem danych do utworzenia modelu, układ tabeli zostanie zmodyfikowany. Najlepszym rozwiązaniem będzie wklejenie danych jako wartości do nowego arkusza. Dane dotyczące roku i miesiąca zostaną połączone w kolumnie data. Dane rozszerzmy o daty dla lat 2015-2016, dla których będziemy prognozować.
Dla tak przygotowanych danych wstawiamy wykres liniowy (zaznaczmy zakres zawierający puste komórki przygotowane dla lat 2015-2016).
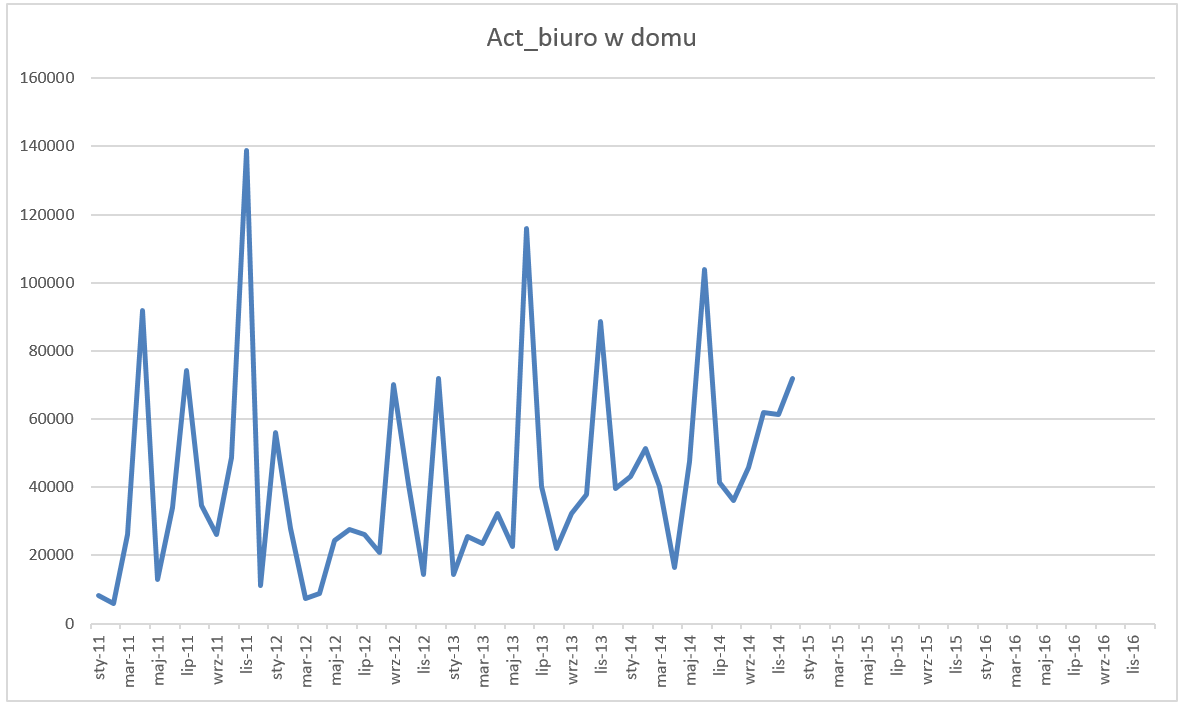
Wykres prezentuje się jak poniżej. Można na nim zaobserwować pewne wahania sezonowe.
Aby zobaczyć tendencję rozwojową dodajmy linię trendu.
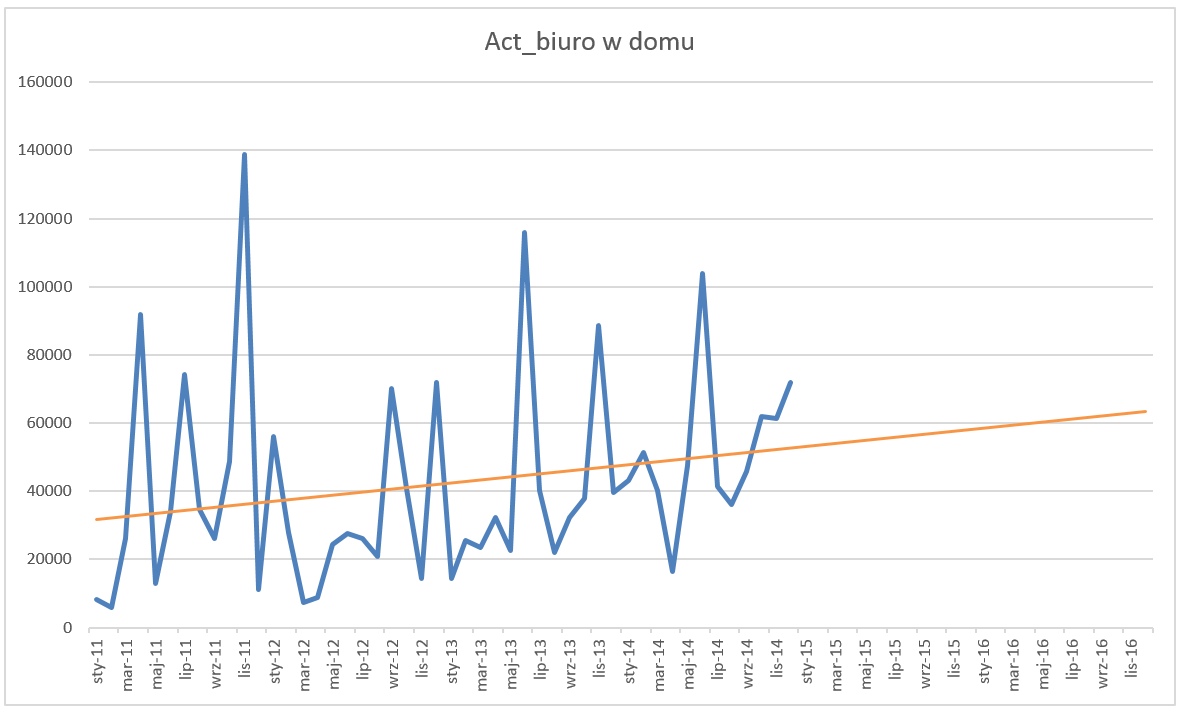
Trend prezentuję tendencję wzrostowa, jednakże nie jest ona tak spektakularna jak niektóre z wyników historycznych i tworzenie prognozy na podstawie linii trendu nie będzie najlepszym rozwiązaniem. Użyjmy zatem bardziej skomplikowanego modelu.
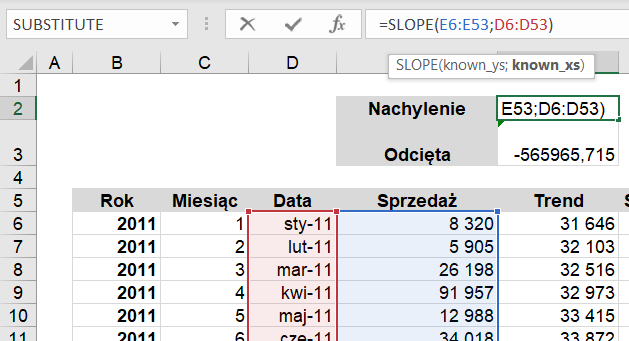
Najpierw przygotujmy dane. Wykorzystamy do tego funkcję Nachylenie. Funkcja ta zwraca nachylenie wykresu regresji liniowej dla wszystkich punktów danych w argumentach znane_y i znane_x. Nachylenie to współrzędna pionowa podzielona przez współrzędną poziomą między dwoma dowolnymi punktami na linii, która określa wielkość zmiany wzdłuż linii regresji. Danymi y będą miesiące, natomiast x – wielkość sprzedaży.
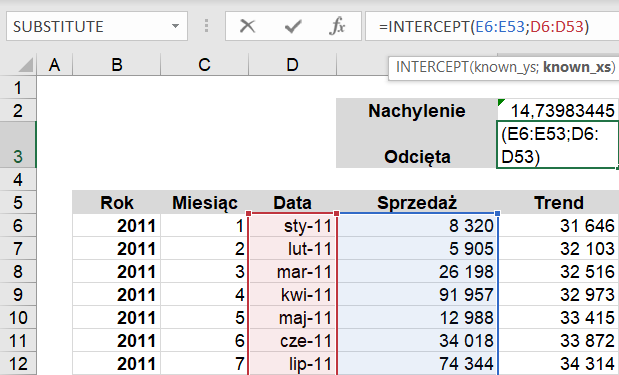
Kolejną wykorzystaną funkcją będzie Odcięta, która oblicza punkt przecięcia się linii z osią y przy użyciu istniejących wartości znane_x i znane_y. Punkt przecięcia jest to punkt, w którym prosta regresji, poprowadzona przez wartości znane_x i znane_y, przecina oś y. Należy stosować funkcję ODCIĘTA wtedy, gdy chce się wyznaczyć wartość zmiennej zależnej przy zerowej wartości zmiennej niezależnej.
Kolejnym krokiem będzie dodanie kolumny Trend.
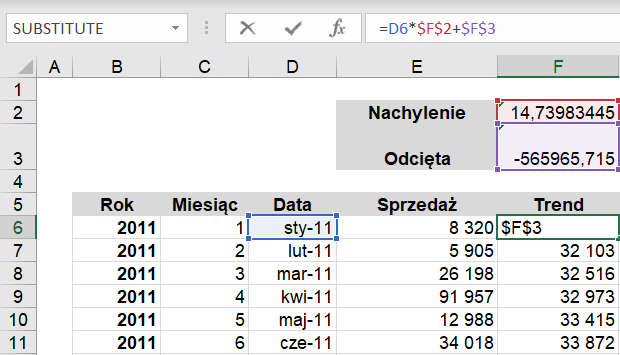
Aby obliczyć wartości trendu wykorzystamy poniższe obliczenie: wartość sprzedaży razy Nachylenie + Odcięta.
Wartości trendu prezentują się jak poniżej.
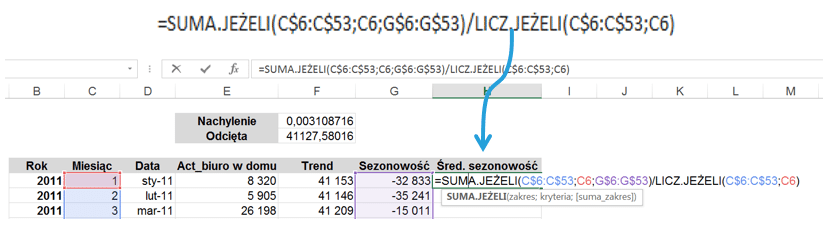
Kolejną dodaną kolumną będzie Sezonowość, która zostanie obliczona jako różnica pomiędzy danymi rzeczywistymi a trendem.
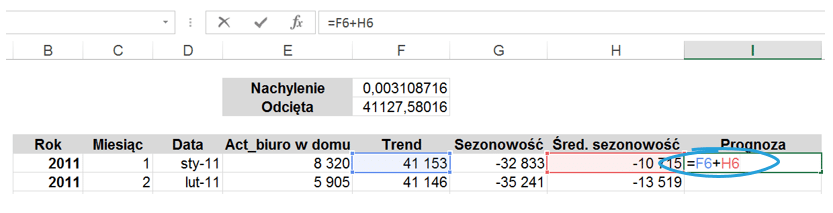
Następnie obliczymy średnią sezonowość dla każdego miesiąca oddzielnie, która będzie bazować na poniższej formule:
Prognoza zostanie obliczona jako suma trendu oraz średniej sezonowości dla danego okresu.
Dodajmy prognozę na wykres (także dla danych historycznych).
Ponieważ przedstawiamy dane nierzeczywiste kolejne elementy wykresu będziemy oznaczać linią przerywaną.
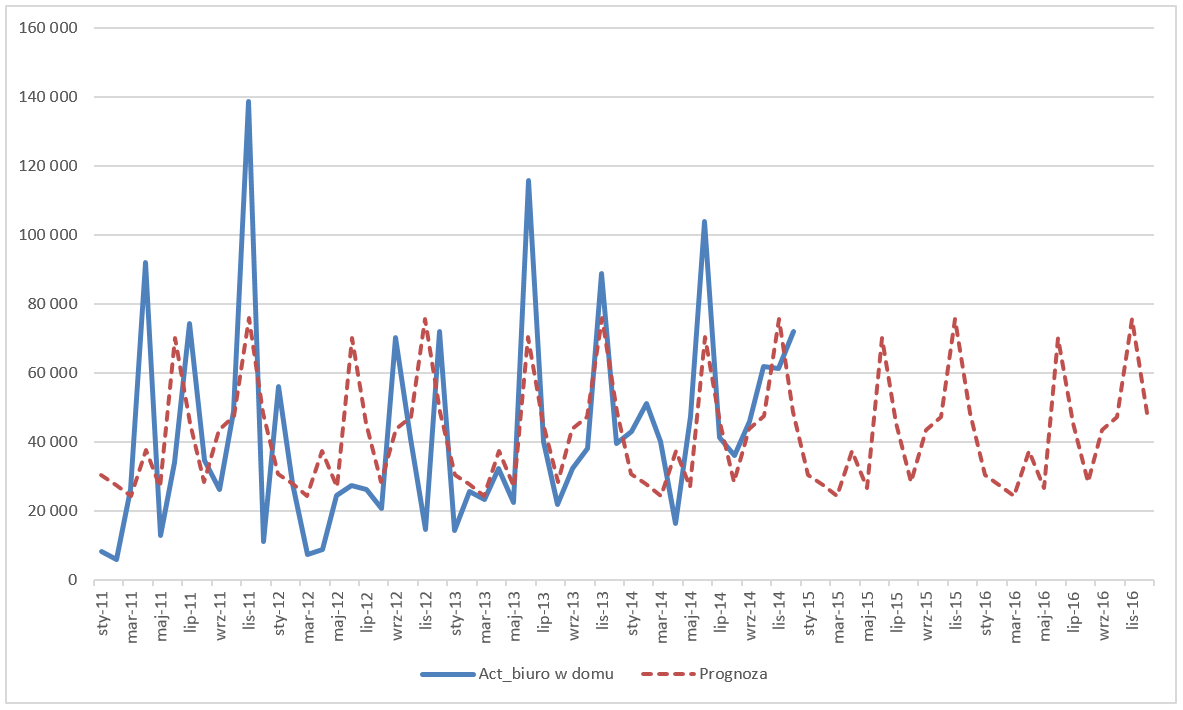
I właściwie taki model i wykres mógłby być tym finalnym. Jednakże uwagę zwraca fakt, że prognoza dla lat 2011-2014 bardzo odbiega od danych rzeczywistych. Dlatego najlepszym rozwiązaniem będzie dodanie do wykresy błędu prognozy.
Model z uwzględnionym błędem prognozy
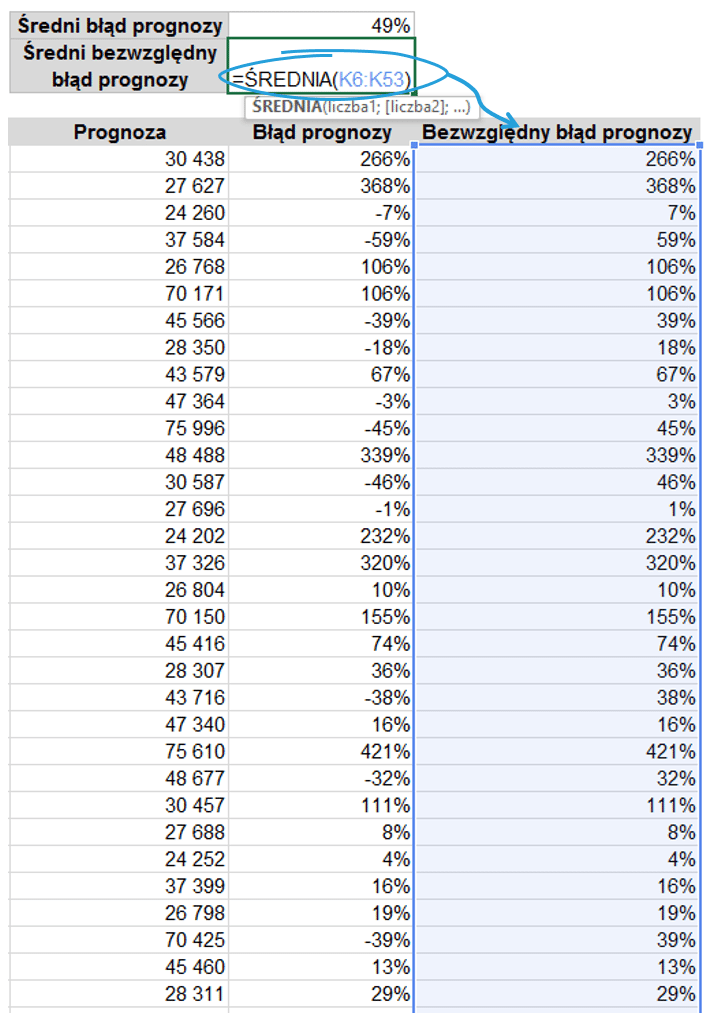
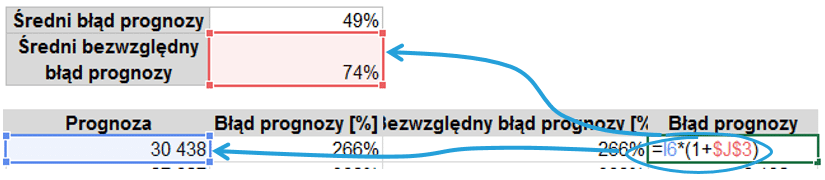
Błąd prognozy można najprościej wyjaśnić jako różnicę pomiędzy danymi rzeczywistymi a danymi prognozowanymi dla tego samego okresu. Błąd prognozy zostanie obliczony jako różnica pomiędzy prognozą a danymi rzeczywistymi podzielona przez wartość danych sprzedażowych.

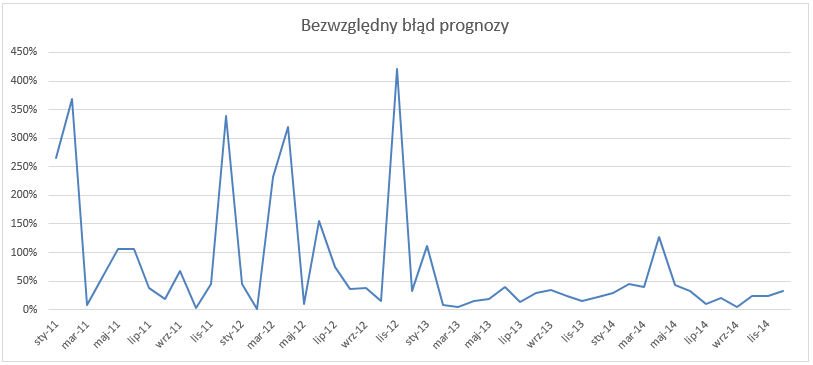
Na podstawie tak obliczonych danych widzimy, że błąd przekracza nawet 400%. Błędy są zarówno wartościami dodatnimi jak i ujemnymi, czyli prognoza została przeestymowana oraz niedoestymowana (estymacja=prognoza).
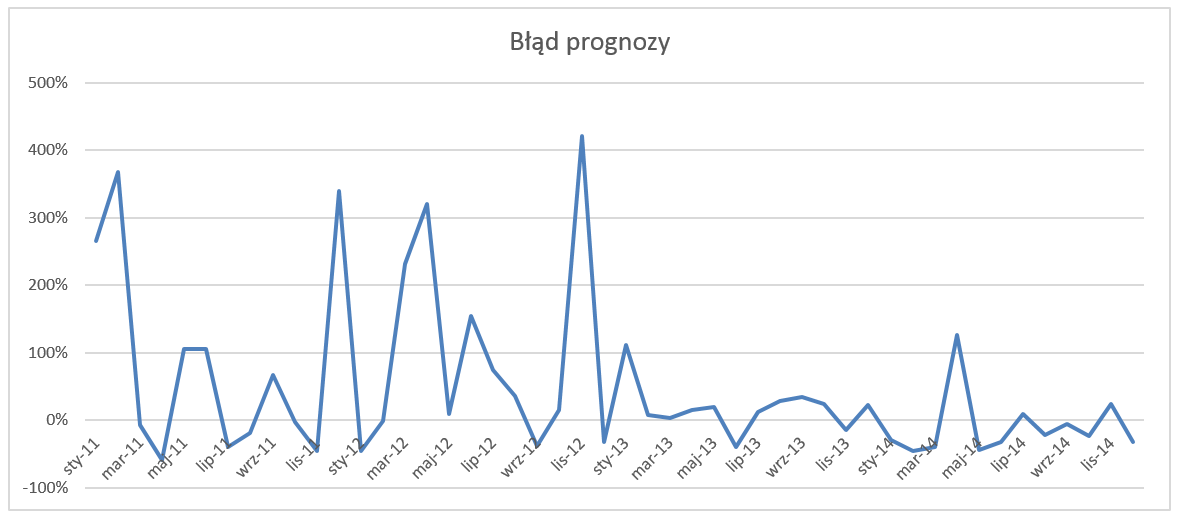
Na podstawie błędu prognozy dla każdego miesiąca obliczmy średni błąd dla całego analizowanego okresu.
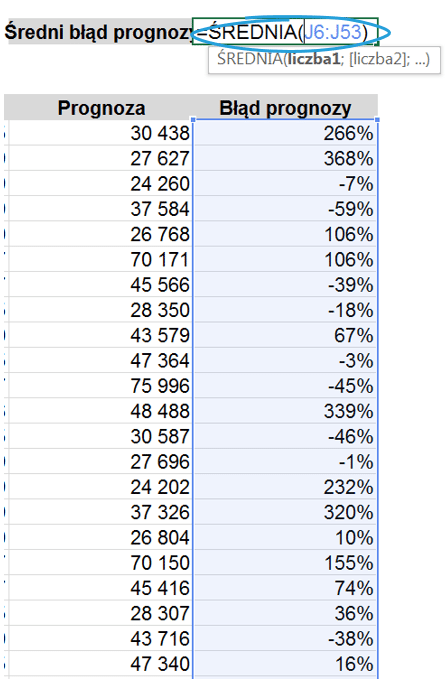
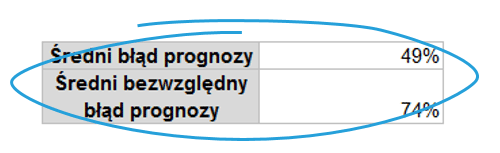
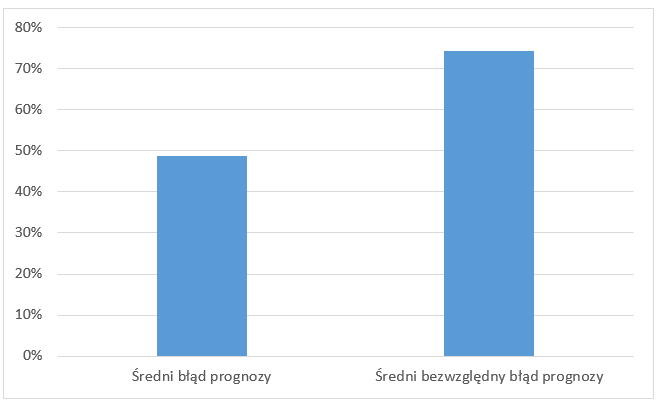
Średni błąd wynosi 49%. Na podstawie wyżej prezentowanego wykresu można uznać to za świetny wynik, zważywszy na fakt, że w niektórych miesiącach błąd wynosi ponad 400%! Z czego to wynika? Taki wynik jest rezultatem uśredniania wartości ujemnych oraz dodatnich, niektóre z nich po prostu się znoszą.
Spójrzmy zatem na bezwzględną wartość błędu prognozy. Do jej obliczenia użyjemy formuły Moduł.Liczby, który zwraca jedynie wartości dodatnie.

Następnie te dane zostaną również uśrednione.
Jak można zauważyć średni bezwzględny błąd prognozy jest znacząco wyższy od uśrednionego błędu prognozy.
Dodajmy do modelu jeszcze jedną kolumnę, która będzie przedstawiać prognozę skorygowaną na plus o uśredniony błąd. Gdyby zależało nam na prognozie in minus, moglibyśmy dodać kolejna kolumnę.
Tak obliczone wartości dodamy jako kolejną serię na wykres.
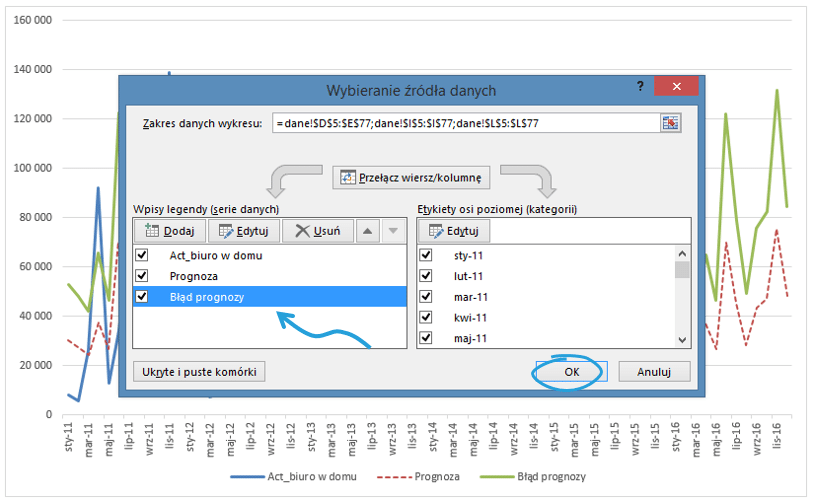
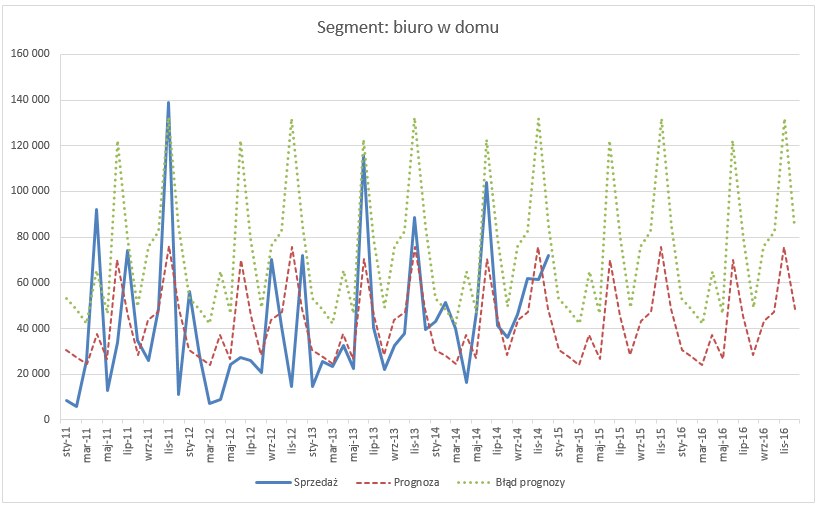
Po sformatowaniu gotowy wykres prezentuje się jak poniżej. Można zauważyć, że prognoza skorygowana o wartość błędu jest zbliżona do danych historycznych.
Wszystkie powyższe operacje powtarzamy dla pozostałych segmentów i formatujemy wykresy odpowiednio, aby otrzymać poniższy wykres panelowy:
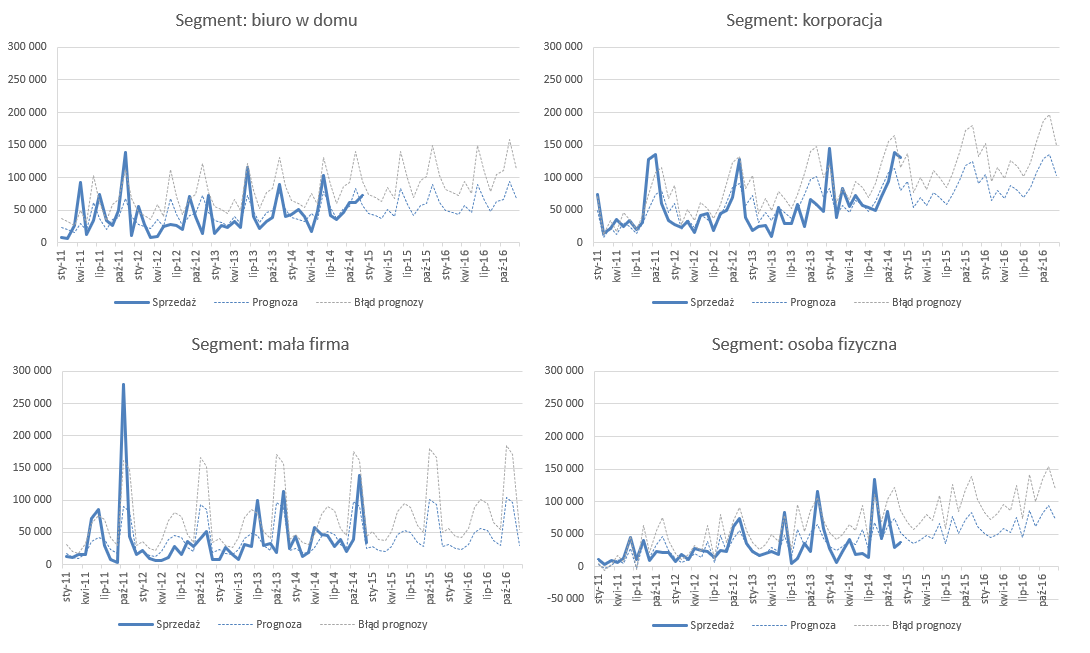
Powyższy przykład obrazuje, jak bardziej zaawansowany model statystyczny pozwala urealnić prognozę, czego rezultatem nie musi być wcale skomplikowana tabela z danymi a prosty wykres z dwiema liniami przerywanymi. Taki pozwala nie tylko szybko zweryfikować poprawność modelu historycznie, ale także planować działania na przyszłość.
Plik do pobrania
Tu możesz pobrać plik źródłowy z modelem szeregu czasowego w Excelu.




wykresy ładne ale prognozy ze średnim błędem na poziomie 75% to bezużyteczne prognozowanie. Kto normalny poważnie weźmie pod uwagę prognozę w której zaprognozujemy sprzedaż na poziomie 50 tys gdy faktycznie będzie ona wynosić 30.
Czy może Pan wskazać źródła/literaturę na bazie której powstało to opracowanie?
Artykuł powstał na bazie: http://www.capacitas.co.uk/blog/forecasting-basic-time-series-decomposition-in-excel
Szanowni Państwo
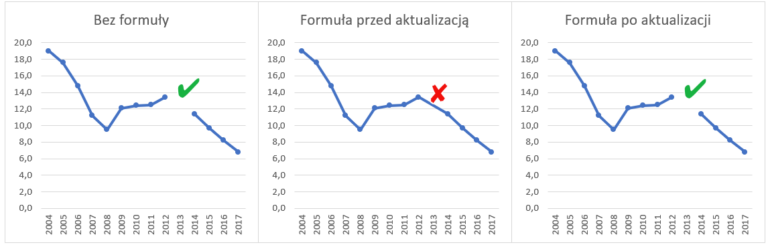
Zwracam się z pytaniem o zasadę wyznaczania wartości trendu. W Waszym przypadku jest to:
przychody * nachylenie + odcięta, czyli to jest jakby trend „daty w zależności od sprzedaży”.
Jak pamiętam, jak się uczyłem o trendach, to wzór wyglądał inaczej:
nr okresu * nachylenie + odcięta, czyli wartość przychodów w zależności od nr okresu.
Oczywiście w moim przypadku inaczej były liczone: nachylenie i odcięta.
Proszę, zatem napisać z czym wiąże się pomysł zamiany osi x na y i y na x?
Poza tym w powołanym przez Was linku podejście do liczenia trendu jest zgodne z moim.
” =A5*C$2+C$3 (multiplying the date by the slope and then adding the intercept) ”
Pozdrawiam serdecznie
Dziękuję za komentarz, który zupełnie zmienił ten artykuł, gdyż dotychczas zawierał on merytoryczny błąd. Artykuł jest poprawiony i liczy teraz nachylenie i odciętą prawidłowo. Zaktualizowałem też plik.
Jakie są źródła opracowywanych danych w tym artykule?
Hej, jakie są źródła opracowywanych danych w tym artykule?
Artykuł powstał na bazie: http://www.capacitas.co.uk/blog/forecasting-basic-time-series-decomposition-in-excel